▼はじめにご挨拶
※3月30日データから考える数学と数式を追加しました。
https://rio2016.5ch.net/test/read.cgi/math/1522017419/
数式では解決出来ない数学的問題でも、実データがを用いる事で解決が
出来る場合があります。
数学の未解決問題のデータを伴う問題として、ABC予想を考えています。

最近のツイッター上でのABC予想関連活動の抜粋です。
https://twitter.com/modulo_p/status/977152622749560833
https://twitter.com/kunne_isepo/status/976512497652936704
https://twitter.com/mat_der_D/status/976744420421681153
強いバージョンの強ABC予想を証明・完成させたい、との思いで2015年から
活動をしています。
ツイッターでは弱いバージョンの弱ABC予想の解説やフェルマーの最終定理の
別証明となる解説をかなり簡単な初等的数学を用いて掲載しています。
強ABC予想の部分的な解は出せているので、クラウドファンディングを通して
共同研究者の方を募り、強いバージョンのABC予想を証明したい、と考えています。
宜しければ、興味のある方は御支援をお願いします。
ツイッターアカウント
https://twitter.com/prime_research1
▼このプロジェクトで実現したいこと
強ABC予想の証明と論文化、共同研究者を探して連携する事で数学的な
未解決問題である強ABC予想を証明・論文化して数学賞の受賞を目指したいと
思います。
数学賞の有名なものはフィールズ賞やアーベル賞、チューリング賞といった
数学賞があります。
▼このプロジェクトをやろうと思った理由
ABC予想は数学的な難問である事に間違いはないのですが、2015年にある
数学問題と巡り合って強ABC予想に繋がる重要な事を見出せました。
ツイッターのフェルマーの最終定理の解説を御覧頂くと一目瞭然なのですが、
数学的な証明を用いなくとも、事象として数学的な未解決問題の説明を結び付
ける事は数学の専門家でなくとも可能なのです。
それは数学ではない、との御意見もあるかもしれませんが、解決出来ていない
数学的問題を解決するには数学的事象の結び付けは効果的な場合があると
確信したからです。
今迄に数名の数学専門家に声を掛けていますが、数学会は権威主義的で実績や
数学的地位がないから、というような理由で門前払い扱いされています。
そこで理論第一主義で行動をして頂ける共同研究者を幅広く探したい、
との思いから、クラウドファンディングを通じて幅広くお知らせするに至りました。
強ABC予想の証明そのものは以前から継続して研究中であり、
クラウドファンディングの成功の有無に関わらず、証明・論文化は実施致します。
▼これまでの活動
平成28年3月度総務省 戦略的情報通信研究開発推進事業 異能vationマッチングプログラム
ブース出展:巨大素数の合成数の効率的解析方法の実践とその周辺理論
平成29年12月度AIST 産業技術総合研究所情報技術研究部門
第9回 暗号及び情報セキュリティと数学の相関ワークショップ ショートプレゼンテーション:約数和からみたABC予想
平成27年6月 アジア人としては初めてビール予想(Beal's conjecture) の一部の解を算出して、AMS(アメリカ数学協会)に投稿、ブログやネット掲示板に同時掲載。残念ながらアメリカで一部の解は先に投稿されていたため、公式なアナウンスはされていない。尚ビール予想そのものは非常に複雑な問題であるため、現在も世界的に完全証明には至っていない。
平成30年2月 ツイッター上でフェルマーの最終定理の別証明に繋がる数論を掲載
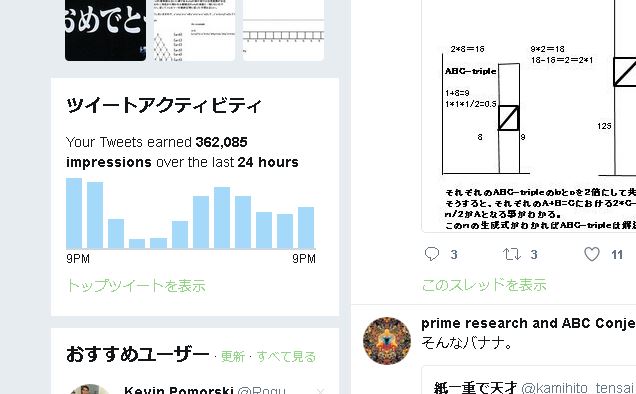
ツイッター上で1日で362085件のインプレッションを得る事が出来ました。
フェルマーの最終定理の別証明を論文化したい方も同時に探しております。
ツイッターアカウント
https://twitter.com/prime_research1
5ちゃんねる掲示板
https://rio2016.5ch.net/test/read.cgi/rikei/1437040101/
・たまに政策的な提言など。上の画像の英文は、現トランプ政権になってから政策
投稿した際の通常の投稿受付メールとは別に、個別の返礼メールで送られてきた
もので、ある日本の政策で採用されています。
▼資金の使い道
演算・記録用のPCの購入や研究への専念活動費(学術関係者ではありませ
んので、今までも全て自己費用)、論文・証明化への費用、及び共著研究
者探しと、その契約費用や共同研究活動費など。
万が一、証明や論文化が成功しなくても、強ABC予想の部分解を基にして
知的財産権の権利を確保しつつ、未完成でも数式の投稿・公表は実施して、
更なる証明の完成度を向上させて行きたいと考えています。
▼リターンについて
3千円でお礼のメールを送信させて頂きます。
1万円で支援協力者グループとして、ツイッター上で掲載させて頂きます(希望者のみ)。
希望される方はツイッターでフォローさせて頂きます。
5万円以上で上記の内容に加えて、論文の作成・申請時にPDF資料をメールにて
配信させて頂きます。
10万円以上で、上記の内容に加えて報告・説明OFF会を開催させて頂きます。
20万円以上で、上記の内容に加えてツイッター上でプレミアムサポートクラブの
会員様とさせて頂きます。
特典として、強ABC予想の証明・論文の共同研究者の方を推薦して頂く事が
出来ます(共著者の方の同意が必要)。
共同研究者の方は、連絡・面談、契約条項に同意を頂いた上で決定させて頂きます。
また、複数以上の方からなる共同研究者者グループとなる可能性もございます。
対象となる方は、整数論に明るく、定義をご自分で考えられる方、新しい定理の
策定を厭わない方、データの分析から数式を算出するのが得意な方、数学的な
論文を書ける方、などが望ましいです。
支援金額が上位TOP3の方は、特別支援協力者として論文上でお名前などを記載
させて頂きます。
強ABC予想の部分的な解は算出できていますので、雲を掴むような困難な
プロジェクトではないかと思います。
ご支援の程、何卒お願い致します。
▼最後に
ABC予想は今迄に証明されていなかった難問に違いはありません。
専門数学者ではないのに、私がビール予想のような数学的問題の部分的な解にせよ、
その解を算出できているのはオーソドックスな数学的手法に依存していないからか
と思います。数学的問題を学問的に証明式で繋ぐのではなく、解を効率的に先に
算出して後から数学的現象を考察する、というような手法ですのでご興味のある
方はツイッターやネット掲示板をゆっくりと御覧になってみて下さい。
時々で思い付いた事を徒然に掲載しておりますので、読みにくい部分があるかと
存知ますが宜しくお願い致します。
最新の活動報告
もっと見る最近のツイッター上でのABC予想関連の出来事
2018/03/24 21:00最近のツイッター上でのABC予想関連活動の抜粋です。 https://twitter.com/modulo_p/status/977152622749560833 https://twitter.com/kunne_isepo/status/976512497652936704 https://twitter.com/mat_der_D/status/976744420421681153 もっと見る
(続き
2018/03/16 05:28さて、ABC予想の問いは前に書いた、任意のεを満たす自然数の組合せ(A,B,C)は高々有限個であろう、となっています。何の事だかさっぱりわかりませんよね。そこで、ABC予想の反例を図形化して、問題の意味をわかりやすくしてみました。 この、ABC予想の反例となるABC-triples、あるいはABC-Hitsと呼ばれるものを簡単な図形にして考えてみましょう。 ABC予想の反例となるABC-triplesやABC-HitsのAの部分の面積を、他のB,Cの数値を直線で図形に表すと次のような図形になります。図の中の頂点にある直角三角形の部分の面積となるAの部分は特徴的であり、Cの直線の長さとBの直線の長さが条件を満たすと弱いバージョンの弱ABC予想の反例が成立する図形パターンとなります。 任意のεを満たす組合せとは、B,Cの線の長さの根基と間隔の比率の事になります。 強いバージョンの強ABC予想の図形パターンも存在しており、この支援プロジェクトはその強ABC予想の証明化を進める国際的な支援プロジェクトとなります。 もっと見る
研究中の成果概要
2018/03/14 19:45ABC予想は考え方によっては、そう難しいものではないのかもしれません。もっとも簡単にABC予想を解説してみます。多くの人による、偉い数学者がたくさんいるのでその内なんとかなるだろう、と思われたABC予想は、出題から数十年が経過しようとしています。 では盲点であったとも思える、簡単な「初等的」解いてみるとは、或いは「強ABC予想」「弱ABC予想」とは、何であるかについて簡単に触れてみました。 ABC予想とは A+B=C となる自然数の関係について述べた数学的な問題です。 例えば、7+23=30 や、1+63=64 といった具合です。 ここでABC予想には約数とか因数分解とかが関係してきます。rad(abc)とは、7+23=30をそれぞれ素因数分解して掛け合わせます。 この時、3*3*3となるような数字になった場合は、3*3を省いて*3とします。すると7*23*2*3*5=4830 となりまして、元のC=30と比べると4830>30であり、 この数値をCに対してのべき乗数εとして、近似値としてのlogで電卓で何乗になるのか計算すると約0.4009615779742 となり、30は4830の約0.4009615779742乗になることがわかります。 おおよその場合は、そのようにA+B=Cを素因数分解した数値の掛け算と、元のCの数値を比べると、素因数分解した数値の掛け算のほうが大きくなります。 では、同じように1+63=64 はどうなるでしょうか。1*7*3*2=42 となりまして、元のCの数字と比べると42<64 で元のCの数字より小さくなってしまいました。 この場合のεは同様にlogで計算すると、64は42の約1.1126941404922乗である事がわかります。 このような元のCの数字に比べて、分解した素因数の積が小さくなる反例が、ABC予想におけるABCトリプルとか、ABCヒットと呼ばれます。 このようなABC予想における反例のεの値が1以上2未満の組合せが弱ABC予想、εが2以上となる組合せを強ABC予想といいます。 もっと見る
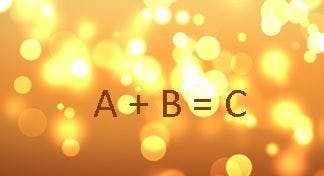













コメント
もっと見る