1. はじめに
錘をエネルギー源とした回転原動機を開発します。この装置(以下 ASLA とします)を利用して発電機を製作します。
2. プロジェクトの目的
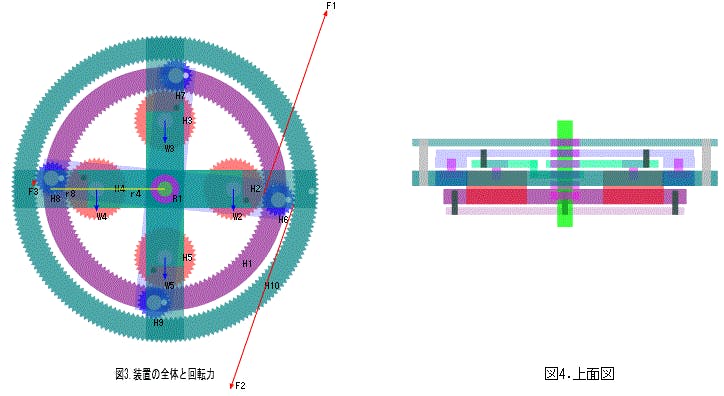
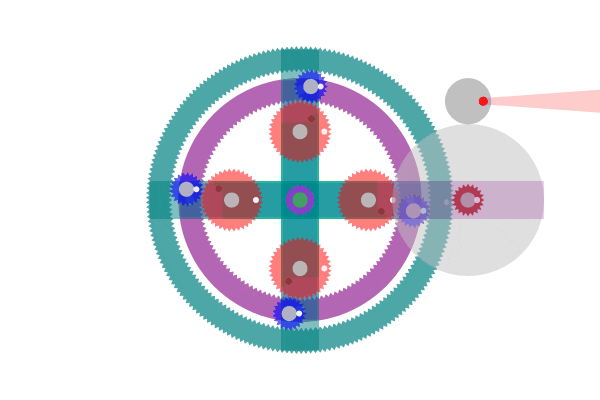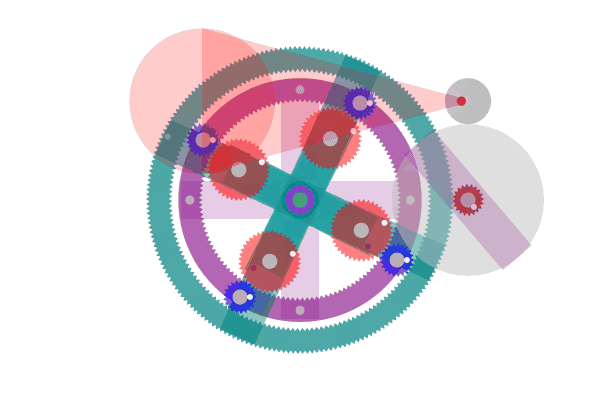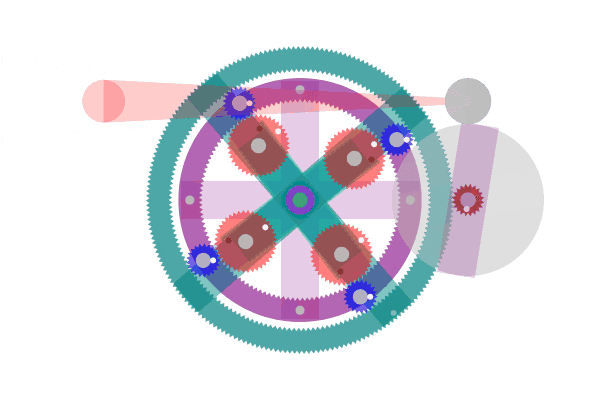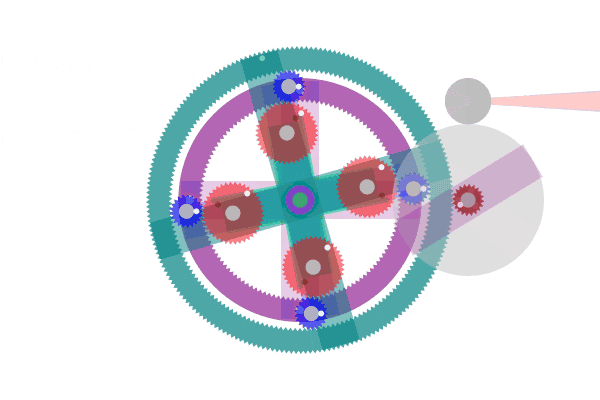
現在の発電機にはガソリン、ディーゼルなどの化石燃料原動機が使用されています。そのために燃料資源枯渇や CO2などの廃棄物の課題を抱えています。ASLAでこれらの課題解決にいくらか役立てればと考えます。図1は装置の回転運動を、図2は吊下歯車単体の振り子運動を示しています。

3. 自己紹介
錘原動機はなかなか出てくる気配を感じられないので2007年頃からどうしたらできるだろう、と思いついたモデルを近所のホームセンターで入手した部材で手作り部品を作成しては色々と試しては、いくつも、いくつもできない物を確認しました。
周りの方々のご意見を伺って次の2つが課題となりました。
1) 錘は高いところから低いところに落下するときにエネルギーを取り出せるけど、一度低いところに落下した錘を元の高いところに戻すときにエネルギーを使用してはいけない。
2) エネルギー保存則で説明する必要がある。
ASLAはこれらの課題を解決したモデルと捉えています。複数の方々から回転継続の評価をいただいております。
4. プロダクトのご紹介
図3 は装置の部品と回転力関係を示します。この装置は固定内歯車の内側に接する吊下歯車が回転軸右側では自由回転落下して、その時に生じる歯車円周上の歯車重量よりも遥かに大きな回転力を逆回転歯車経由で一番外側の伝達歯車に伝えて安定位置の回転軸真下に向かって回転落下します。一方、回転軸左側では吊下重量は接続棒に乗りかかり自由回転落下せずに、ただの接続棒に固定されて空転状態となり回転力差異から安定位置の回転軸真上に向かってエネルギーを消費しないで回転上昇します。
F1 は W2重量 から発生する H2.吊下歯車の自由回転落下力が伝わる H6.逆回転歯車の時計回り回転力です。F1 の矢印長さは図外に飛び出してしまうので 1/4 の長さで示してあります。実際はこの長さの 4倍 となります。F2 はこれが H10.伝達歯車 に伝わる時計回り回転力です。
F3 は W4重量 から発生する H10.伝達歯車 の反時計回り回転力です。吊下歯車は回転軸の左側では逆回転歯車に固定された N1.接触棒 に乗りかかるので回転落下力は無くなり、接続棒を経由して H8.逆回転歯車 に W4重量 は伝わります。それで r4 は R1 から H4.回転軸距離、r8 は R1 から H8.回転軸距離とすると、F3 = W4 * r4 / r8 / 2 となり、およそ W4 / 4 と装置サイズが大きくなってもそれほど変化がありません。
F2 は F3 の 227.79 倍となり、F2 > F3 の関係から H10.伝達歯車 は静止状態から時計回りに回転を開始して、回転力の差は常時伝達歯車に伝わるので回転速度は徐々に速くなり、やがて最終回転速度で 図1 のように 回転運動を継続します。H10.伝達歯車 の外側に一個から複数個の発電機を取り付ければ、昼夜天候に関わらずに常時安定して燃料を消費せずに不要廃棄物を発生しない安全性、経済性、安定性に優れた電力を入手できます。図4は装置の上面図を示します。
5. 錘を点ではなく円盤として取り扱います
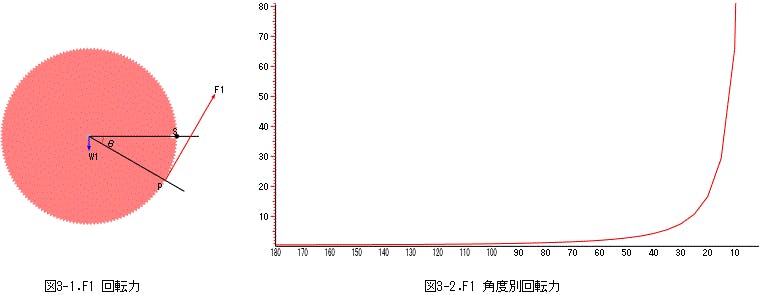
図3-1 は吊下歯車の回転軸水平線右側円周上の点 S を支点として角度 θ の円周上の点 P に生じる歯車重量 W1 による円周接線方向の回転力 F1 を示します。 図3-2 はこの F1 の間隔角度別推移を横に間隔角度、縦に W1 の倍数で示します。 F1 は 180°の W1/2 から始まり、水平間隔角度が小さくなると図のように急激に上昇するので、この回転力を原動力として利用します。
6. 表1-3 歯車 ( モジュール = 1 )の使用

7. 表1-4 回転力の比較

8. こだわり・特徴
化石燃料原動機では燃料を使用しているので、騒音や振動、排気ガスの課題があり、定期的に燃料補給を必要とするのでそのための作業と費用、燃料貯蔵空間を必要とします。また火災や爆発の危険性があります。
ASLAはこれらの課題を解決して昼夜天候に関わらずに安定して稼動します。
回転力を上げるには錘重量を増やす、装置を大型化するなど、それ程複雑ではない作業で行えます。大きくすると相対的に相手発電機の回転数が増大します。
9. プロダクト誕生までのお話
高いところから低いところに落下した錘のエネルギーを取り出した後、再び元の高いところに錘を戻す時にエネルギーを消費せずに行う方法をしばらく考えました。日数はかかりましたが2個の錘を別々に落下させる時に「てこ」を利用して機能していない重心を回転軸の上方に持ち上げてから、一本の棒に2個の錘を乗せれば重心が機能するので勝手に落下する、というモデルと出会いました。この頃からこのモデルの実現方法を色々と試作してきました。各必要部位の回転力をばね秤で測ると計算値には程遠い計測値ですが回転可能な数値は確認できました。きちんとした歯車を使用した試作機にて結果を確認します。
10. 会社・チームの紹介
専門の機械装置メーカー様と装置仕様内容、製作工程について十分意見交換させていただいてより優れた装置製作に勤めます。
11.資金の使い道について
以前のもう少し複雑なモデルで製作依頼したときの見積費用を参考にしております。
装置設計費:約 80万円
装置製作費:約400万円
発電機関係機器購入加工費:約80万円
装置試験費:約 80万円
CAMPFIRE掲載手数料・決済手数料:約 160万円
12. Q&A
Q1.錘は高いところから低いところに落ちるときにエネルギーを入手できるけど、一度落ちた錘を低いところから高いところに戻すときにエネルギーを消費しているのではないですか。
吊下歯車は回転軸右側では自由回転落下して回転軸真下の安定点に向かって回転落下します。回転軸左側では自由回転落下せずに逆回転接続棒に乗るので、伝達歯車回転力差から回転軸真上の安定点に向かって回転上昇します。このときにエネルギーを消費してはいません。
Q2.永久機関だから実現不可能なものではないですか。
装置外部からエネルギー源を供給されずに装置外部へはエネルギーを供給することになるので第一種永久機関に該当するのでしょうか。
Wikipedia では
「永久機関が実現すれば石炭も石油も不要となり、エネルギー問題など発生しない。18世紀の科学者、技術者はこれを実現すべく精力的に研究を行った。しかし、18世紀の終わりには純粋力学的な方法では実現不可能だということが明らかになり」
とあります。永久機関に該当するかどうかは専門の方のご判断を待ちます。
回転継続の可能性を感じておりますので試作機にて動作を確認いたします。
Q3.エネルギー保存則ではどのような説明になりますか。
エネルギー保存則は「孤立系のエネルギーの総量は変化しない」という物理学における法則の一つである、とあります。
この装置ではエネルギーを生成して外部に出力していますが外部から投入するエネルギー源がありません。
装置全体を 1個の「系」とするとこの装置はこの法則に不合理となります。
そこで、「振り子運動では位置エネルギーと運動エネルギーの総量は変化しません」とあるので振り子運動を「系」とします。
H2,H3,H4,H5.吊下歯車4個の振り子運動から装置には4個の「系」を用意します。
吊下歯車は回転軸右側では回転落下する振り子運動を行い「系」が活動状態となりますが、回転軸左側では吊下歯車保持接触板に接触して振り子運動が無くなり「系」が休止状態となり活動状態にある「系」の作用により自動的に安定する最上位置に回転上昇します。
このように休止状態「系」のときに他方活動状態「系」の作用によりエネルギーを消費しないで増大した位置エネルギー源を、活動状態「系」のときに運動エネルギーへの変換を交互に繰返すことで、装置外部からエネルギー供給を必要としないで装置外部へは運動エネルギーを供給することが説明できるようになります。
<All-in方式の場合>
本プロジェクトはAll-in方式で実施します。目標金額に満たない場合も、計画を実行し、リターンをお届けします。






コメント
もっと見る