「普通のバブルソートと普通ではないバブルソート」に挙げた “pat” は3次元の配列でした。ここで、すこし見てみましょう:
pat = [
　[[2, 1], [1, 2]],
　[[3, 1], [1, 3]],
　[[4, 1], [1, 4]],
　[[5, 1], [1, 5]],
　[[6, 1], [1, 6]],
　[[7, 1], [1, 7]],
　[[8, 1], [1, 8]],
　[[9, 1], [1, 9]],
　[[3, 2], [2, 3]],
　[[4, 2], [2, 4]],
　[[5, 2], [2, 5]],
　[[6, 2], [2, 6]],
　[[7, 2], [2, 7]],
　[[8, 2], [2, 8]],
　[[9, 2], [2, 9]],
　　[略]
　[[7, 6], [6, 7]],
　[[8, 6], [6, 8]],
　[[9, 6], [6, 9]],
　[[8, 7], [7, 8]],
　[[9, 7], [7, 9]],
　[[9, 8], [8, 9]]
]

これだとわかりにくいかもしれませんが、この “pat”が3次元の配列だということは、「普通のバブルソートと普通ではないバブルソート」に挙げた後者のプログラムのこんなところで確認できます:
　　　　if data2 == pat[k][0]: 　　　　# C
　　　　　data1[i] = pat[k][1][0]
　　　　　data1[i+1] = pat[k][1][1]
　　　　　print("FIND", data2, "->", pat[k][1])

ここで、“data1[i] = pat[k][1][0]” として、たとえば “[[2, 1], [1, 2]]” という要素の、 “[1, 2]” の、 “1” などにアクセスしています。添字が “[k]”、 “[1]”、 “[0]” と3つあり、それで表記上の最深部の要素にアクセスできていますから、3次元であることは問題なく理解できるかと思います。

さて、この “pat” ですが、配列であるとともに、リストでもあります (すくなくともPythonの用語としては)。実際、 "pat.append([[10, 9], [9, 10]])” とすると、上に示したものの最後に “[[10, 9], [9, 10]]” が追加されます。このように、大きさが可変なのはリストの特徴でもありました。

ところで、配列というと、その要素へのアクセス方法、あるいは表記の方法としては、 “pat[k, 1, 0]” という形も一般的です。なぜ、この “pat” では “pat[k][1][0]” という表記になっているのでしょうか。

答えの一つは簡単で、 “pat” の “k番目の要素” の、 “1番目の要素” の、 “0番目の要素” にアクセスするという書き方だからです。あるいは別の答としては、“pat” というオブジェクト (ここではリスト) の “k番目のオブジェクト (ここではリスト)” の、 “1番目のオブジェクト (ここではリスト)” の、 “0番目のオブジェクト (ここでは整数)” にアクセスするという書き方とも言えます。

Pythonのソースコードをきっちり見たことはありませんが、Rubyは、ネット・ニュースにソース・コードが流されていた時代に、ちょっと覗いたことがあります。Rubyの場合、上の例に出てくる “[” や “]” もメソッドとして定義されています。そこで、 “[” あたりの定義をRuby自身で書き換えてやることで、私は連想配列を実装していました。これは、当時、私はjgawkに慣れ親しんでおり、「連想配列、便利だなぁ」と思っていたことからやったことです (多次元配列はどう書くんだろうと思ったからという理由もあったことは内緒です)。ですが、これができるということは、Rubyはオブジェクト指向であることを徹底していることの証左とも言えるでしょう。

さて、この “pat” は、同時に木構造でもあります:

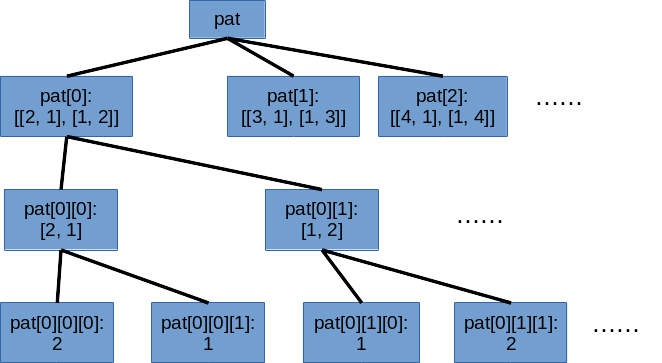
普通の配列、つまりはメモリ領域をいっぺんに確保するような配列では、その個々の要素の間にはこのような入れ子の関係はありません。このような図示が可能なのは、リストの入れ子の形で配列を実現しているからです。(もちろん、普通の配列でも、入れ子であると意識して(思い込んで)扱うことは可能です。)

リストの入れ子は、自然と木構造にもなります。では、木構造はリストの入れ子の形でしか現わせないのでしょうか。もちろん、そんなことはなく、普通の配列でも現わせます。ですが、その紹介は後の機会にとさせていただきます。