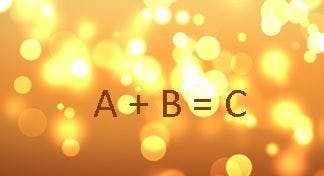最近のツイッター上でのABC予想関連活動の抜粋です。 https://twitter.com/modulo_p/status/977152622749560833 https://twitter.com/kunne_isepo/status/976512497652936704 https://twitter.com/mat_der_D/status/976744420421681153

さて、ABC予想の問いは前に書いた、任意のεを満たす自然数の組合せ(A,B,C)は高々有限個であろう、となっています。何の事だかさっぱりわかりませんよね。そこで、ABC予想の反例を図形化して、問題の意味をわかりやすくしてみました。 この、ABC予想の反例となるABC-triples、あるいはABC-Hitsと呼ばれるものを簡単な図形にして考えてみましょう。 ABC予想の反例となるABC-triplesやABC-HitsのAの部分の面積を、他のB,Cの数値を直線で図形に表すと次のような図形になります。図の中の頂点にある直角三角形の部分の面積となるAの部分は特徴的であり、Cの直線の長さとBの直線の長さが条件を満たすと弱いバージョンの弱ABC予想の反例が成立する図形パターンとなります。 任意のεを満たす組合せとは、B,Cの線の長さの根基と間隔の比率の事になります。     強いバージョンの強ABC予想の図形パターンも存在しており、この支援プロジェクトはその強ABC予想の証明化を進める国際的な支援プロジェクトとなります。    

ABC予想は考え方によっては、そう難しいものではないのかもしれません。もっとも簡単にABC予想を解説してみます。多くの人による、偉い数学者がたくさんいるのでその内なんとかなるだろう、と思われたABC予想は、出題から数十年が経過しようとしています。 では盲点であったとも思える、簡単な「初等的」解いてみるとは、或いは「強ABC予想」「弱ABC予想」とは、何であるかについて簡単に触れてみました。 ABC予想とは A+B=C となる自然数の関係について述べた数学的な問題です。 例えば、7+23＝30 や、1+63＝64 といった具合です。 ここでABC予想には約数とか因数分解とかが関係してきます。rad(abc)とは、7+23＝30をそれぞれ素因数分解して掛け合わせます。 この時、3*3*3となるような数字になった場合は、3*3を省いて*3とします。すると7*23*2*3*5＝4830 となりまして、元のC=30と比べると4830＞30であり、 この数値をCに対してのべき乗数εとして、近似値としてのlogで電卓で何乗になるのか計算すると約0.4009615779742 となり、30は4830の約0.4009615779742乗になることがわかります。 おおよその場合は、そのようにA+B=Cを素因数分解した数値の掛け算と、元のCの数値を比べると、素因数分解した数値の掛け算のほうが大きくなります。 では、同じように1+63＝64 はどうなるでしょうか。1*7*3*2＝42 となりまして、元のCの数字と比べると42＜64 で元のCの数字より小さくなってしまいました。 この場合のεは同様にlogで計算すると、64は42の約1.1126941404922乗である事がわかります。 このような元のCの数字に比べて、分解した素因数の積が小さくなる反例が、ABC予想におけるABCトリプルとか、ABCヒットと呼ばれます。 このようなABC予想における反例のεの値が１以上２未満の組合せが弱ABC予想、εが２以上となる組合せを強ABC予想といいます。