本解説の執筆とやたらにやっているオルガノンクラスそれ自体の宣伝が忙しく体力的に限界なので、この活動報告を通して被覆空間の解説をすることをやめます。

今までの記事と合わせて、残りの記事も2020年4月以降、書き直したものをわたしのブログに掲載する予定ですので、もし楽しんでいた方がいらしたら、そちらをお待ちください。

以下、下書きだけ、貼り付けておきます。mdソースのままですが……

予定されていてもの

# 普遍被覆と被覆変換群の話そのに: CAMPFIRE

## 目次

1. 被覆空間の概略 

2. 位相空間と基本群

3. 普遍被覆空間と被覆変換群そのいち  (この記事) 

4. 普遍被覆空間と被覆変換群そのに

5. 被覆空間のガロア理論素描

番外編1. 群の話

番外編2. 体と群の対応

## 被覆変換群

平行移動をつぎのように一般化して考える。

(Y, p) を X の被覆空間とする。 Y から Y への同相写像 φ であって、  φ; p = p なるものを被覆変換といい、その全体を Aut(p) を表し、被覆変換群という。ただし、 ";"で関数の合成を表している。

図3b-1

Aut(p) はその名の通り、群になる。

Y を X の被覆空間とし、 X の点 x0 を考える。 X の x0 を基点とするループは、 Y では x0 のファイバー内の二点の間の道になる。なお、もちろん終点も一致していたらループを定める。

このことから底空間のループから普遍被覆空間での被覆変換を作れます。

さらに、X の普遍被覆 (Z, q) を考え、 Aut(q) をとる。X 内の非自明なつまり「一点に連続変形で潰れない」ループは Z 内で X のコピーから別のコピーへ移動する道と解釈され、 Aut(q) に属する。自明なループは、 Z では閉曲線と解釈され、 Aut(q) の単位元になる。

つぎの図は、円柱とその普遍被覆R × Dで被覆変換とループの関係を示しています。

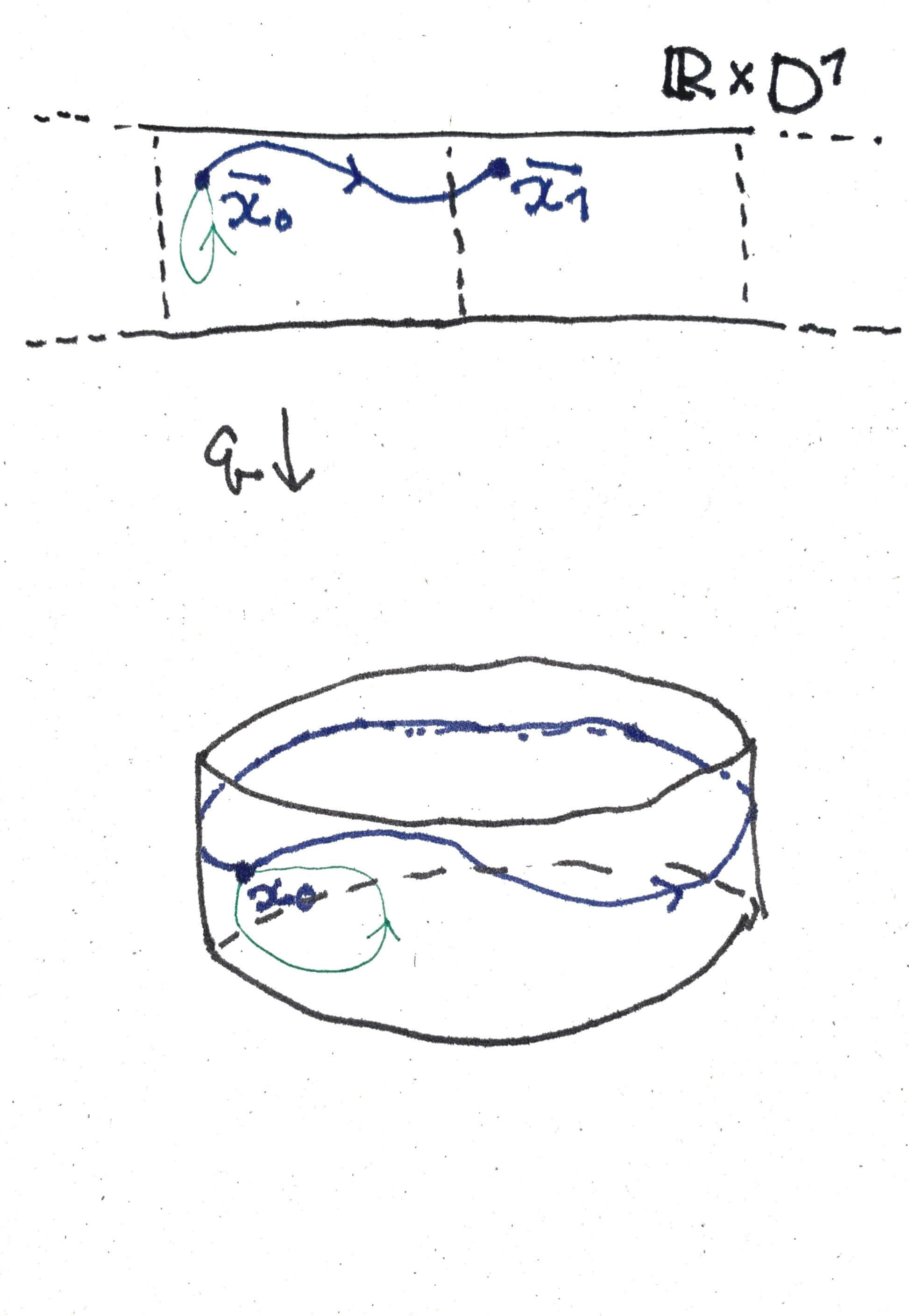図3b-2

このように普遍被覆 (Z,q) で異なる被覆変換が底空間 X の異なるループに対応します。

以上を合わせて、底空間の基本群 π(X) は、普遍被覆空間の被覆変換群 Aut(q) との間に一対一対応を持ち、さらに群として同型、つまり同じかたち・構造を持ちます。

したがって、つぎの結論を得ます。

(Z, q) を X の普遍被覆とし、 x0 を X の点とする。このとき、 π (X, x0) と Aut(q) は群として同型である。

これを用いると、普遍空間の被覆変換群を通して底空間の基本群を計算できます。

クラインの壷 K を例に計算してみましょう。

* Kの構成

* R × R が普遍被覆であること; q の構成

* Aut(q) の計算