論理演算をそのまま考えるとか憶えるというのは、どれくらい意味があるのかなとは思います。ですが、プログラミングにおいてand、or、notは、条件文あたりで普通に使いますので、どうにかして触れないわけにもいかないとも言えるかもしれません。表をそのまま憶えるのが一番簡単ではあると思うのですが。

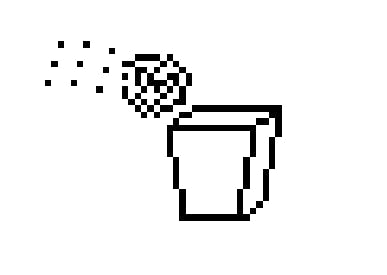
このあたりの論理演算だと、ガジェット・コンピューティングのような感じで作ってやることもできます。そんな一例は、次のようになります。上から順番に “and”、 “or”、 “not”です:

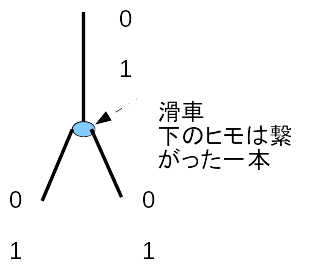
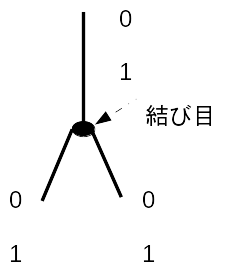
これらの図を見てもらった上で、まず、“and”、 “or”、 “not” の論理演算がどういうものかを確認します。

“and”:
入力Ａ　入力Ｂ　出力
　０　　　０　　　０
　０　　　１　　　０
　１　　　０　　　０
　１　　　１　　　１

“or”:
入力Ａ　入力Ｂ　出力
　０　　　０　　　０
　０　　　１　　　１
　１　　　０　　　１
　１　　　１　　　１

“not”:
入力　出力
　０　　１
　１　　０

これらを確認していただいた上で、上の図についてすこし説明をすると、 “and” の場合、下の片方の紐を引っぱっても、滑車を通ってもう片方の紐がでてくるだけです。両方の紐を引っぱると、そういうことにはならず、装置全体が下に引っぱられ、上の方の紐なのか棒なのかの位置が “1” になります。

“or” の場合、滑車ではなく結び目になっているので、下の片方の紐を引っぱれば、装置全体が下に引っぱられ、上の方の紐なのか棒なのかの位置が “1” になります。

“not” の場合は、軸にバネがついた腕木を用います。最初の状態では、左下の棒かなにかの位置は、 “0” であるのに対し、右上の方は “1” になっています。ここで、左下の棒かなにかを引っぱると、左下の位置は “1” になるのに対して、右上の位置は “0” になります。

と、1桁の “and”、 “or”、 “not” は、こんな感じのガジェットで実現できます。これは、説明には使えるかもしれませんが、論理演算を実際に理解できることに繋がるかというと、疑問ではあります。児童・生徒に面白いと思ってもらえるかも、正直なところ疑問です。

あまり複雑になっても、理解からは遠ざかるのではないかと思いますが、ガジェトを使う/使わないは検討の課題に残すとして、2bitどうしの加算回路 (桁上げフラグ付き) くらいは、動作を試し、児童・生徒にも体験してもらい、理解してもらうことを実現したいと考えています。

興味を持たれましたら、ぜひご支援や、コメントをお願いいたします。

プロジェクトの本文や、活動報告についての感想、ご意見、ご質問を、ぜひコメントでお寄せいただければと思います。現在は支援募集期間中であり、本企画の実施期間ではないため、お寄せいただいた感想などについてはリターンとしてではなく、お返事や回答をさせていただきます。

また、私個人についてはこちらをご覧ください。