クラウドファンディング募集期間：2022/8/31まで

https://camp-fire.jp/projects/view/601765

＜今日イベントが終了します。ご支援お願いいたします＞

　現在、第一章の小学校から中学3年分の計算の分を作っています。この講座では応用問題をできるようにすることを主眼を置いています。複数の条件を一緒くたにぐじゃぐじゃに考えているから出来ないんです。その着眼点は「問題文を分解し数式へ変換(翻訳)」と「その数式を機械的に計算」を明確に分離することです。「数式の計算」はルールにのっとったゲームと考え、理屈よりもイメージを作ってもらおうと考えています。計算ルールを「スライド」 主体に学習し、わからない点を「動画解説」で補足、 「クイズ」 で定着という構成にいたします。教科書には載っていない秘策もお教えしますので、計算速度が飛躍的に上がると期待してください。
　第二章以降は翻訳に主軸を移していきますので、これより先、数学コンプレックス解消につながる結果が出せるよう講座を作っていくつもりでおります。この部分が現在ほぼ誰も結果を出せていない部分です。期待してください。

　学習塾の提供する高校受験という短期的なコストパフォーマンスとこのプロジェクトが目標とする生涯賃金ややりがいのある仕事という生涯にわたるコストパフォーマンスをてんびんにかけるという当事者であるこどもが気づかないことを大人たちが教えてあげる必要があると思います。 (8/31追記) 

講座資料の一部を活動報告で公開中。リンゴとバナナから始めますので、小学生でも始められます。

分数のたし算の原稿の一部を活動報告に記載しました。(8/12追記) 

「算数と数学の違い」の原稿の一部を活動報告に記載しました。多くの方がわかっていない項目です。(8/9追記) 

時間割を作り決まった時間に机につかせるようにしてほしいという要望がありました。時間予約を選択できるようにいたします。(8/9追記)

こどもとのコミュニケーション手段として。(8/8追記) 

今回のミサイル発射について思うこと。台湾問題と私(1996年 )と娘(2022年)。活動報告に記載しました。(8/7追記)

今春、文系大学に入学された若者からコメントを頂きました。すごい文章力です。活動報告に記載しました。(8/6追記)

　はじめまして、昨年還暦を迎えました元物理学研究者の由利正忠と申します。

　まだ台湾の研究所に勤務していたころのことです。教えることが好きだった私は、直属の上司である研究所所長に大学生を指導したいので帰国したいと相談したことがあります。そのとき所長からこう言われました。「大学生を教えるんじゃなくて、中学生を教えたら。」そのときは、何を言っているのか理解できませんでした。時が過ぎ、娘の高校受験もあり、市販５社の都立高校入試過去問集を比べて見ることにしました。「この解説で解けるようになる子はいったい何人いるんだろう」と感じたことから、都が発表している正答率の統計を取りグラフ化して見たんです(詳細後述)。ここで初めて研究所長の伝えたかった事が分りました。大学ではもう遅すぎる。中学数学が日本の教育の最大の問題点だったんです。数学コンプレックスも理系離れも全てここから始まっていたんです。

　ところで、あなたはお子さんに将来どんな風になってもらいたいと思っていますか？
「こどもたちには無限の可能性がある」とかよく言われています。でも、理系離れが問題となっている今、数学が苦手というだけで、その選択肢は大幅に狭まってしまいます。中学生の段階で将来に制限がかかってしまう。数学コンプレックスが収入に大きく関係しているという研究もあります(後述) 。あなたのお子さんにチャンスを与えて上げてください。数学コンプレックスの解消こそが最も効率的で効果的な方法だと考えます。実際、中学数学は将来をあきらめなければならないほど難しくはないんです。
　こどもたちに数学って本当は「簡単で面白いんだ」って思ってもらいたい。数学を好きになって理工系に進学する子たちに、技術立国日本の未来を託したい。その目的のために中学数学講座を作ります。中学生だけでなく、中学数学を学びなおしてみようかなって思われる方も物の見方が変わると信じています。

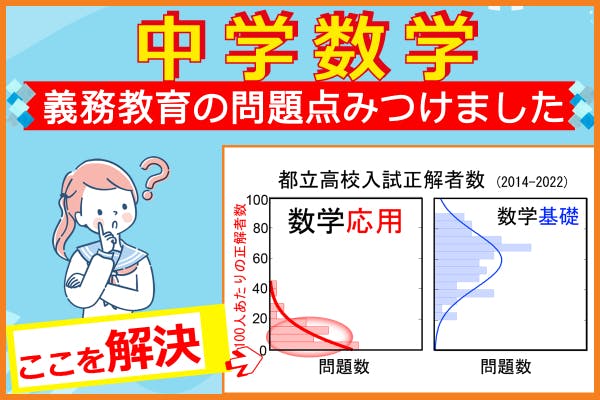
　数学の学習塾はいっぱいあるのになぜ今更「あなたが教える必要があるのか」と思われる方へ、今の学習塾が「中学数学」に対して十分には機能していません。その証拠として、過去９年間の都立高校入試問題の正答率の統計をお見せします。東京都教育委員会が毎年公表している正答率をまとめたグラフで、左端がほぼ全員不正解(100人当たり95人以上不正解)、右端がほぼ全員正解(100人当たり95人以上正解 ) 、縦軸は問題数です。数学は毎年19問中4問が応用問題です。漢字5問と計算6問は多くの受験生が好成績だったため別統計にしました。
　以前から感じてはいましたが、実際に統計を視覚化してみると信じがたい状況になっていました。教育問題として取り上げられた覚えがないのですが、おそらくこのような切り口で統計を分析しなおした人は今まで誰もいなかったのではないでしょうか。もし過去に誰かが提示していたとしたら、何度もおこなってきた教育改革の中で何らかの策を講じているはずです。「数学だけ」が国、英、社、理と違う。応用問題ができない生徒「がいる」ではなく、ほんの一握りの数学が得意な生徒を除き応用問題ができない生徒「ばかりいる」という結果になっています。すべての入試科目の中で数学応用問題だけが正解できていない、つまり、習得できていないという統計結果です。都立高校を受験していない生徒は含まれていませが、統計として充分意味のある35万人以上の受験生の、しかも学習塾の最も多い東京都の公式な試験結果です。この結果をまず認めてください。　数学応用問題を全生徒ができるように教育することはできませんが、数学応用問題が全くできないという現状はすぐに改善しなければなりません。出題レベルを落とさずに、平均として少なくとも3分の１の生徒が正答する上記のような分布になるようにする教育目標を立てる必要があると考えます。日本は理系の人材を必要としていると私は考えています。外国に頼らず国内での理系人材育成のため、中学数学応用問題が出来ていないという事実を社会問題として広め、改善を促す努力をしてまいりますので、ご協力いただきたくお願いいたします。この目標を達成するための私なりの手段と内容を説明していきます。

　これまで何度も教育改革がなされています。今でもいろいろな方面から問題が提案されていることでしょう。しかし、義務教育段階の学力面で、唯一中学数学の改善がなされてはいなかったという事実が示された以上、ほかのどの問題よりも早急に取り組まなくてはならない問題だと私は考えます。皆さんはどう思われますでしょうか。中１ギャップという言葉もあり、他の科目に比べ数学が中１生徒にとってとびぬけて苦手な科目になっています。完全に小学校からの引継ぎに失敗しています。中学数学でつまずいた子たちを引継がなければならない高校や予備校の数学教師たちは既に諦めてしまっている生徒に対し授業をしなければなりません。

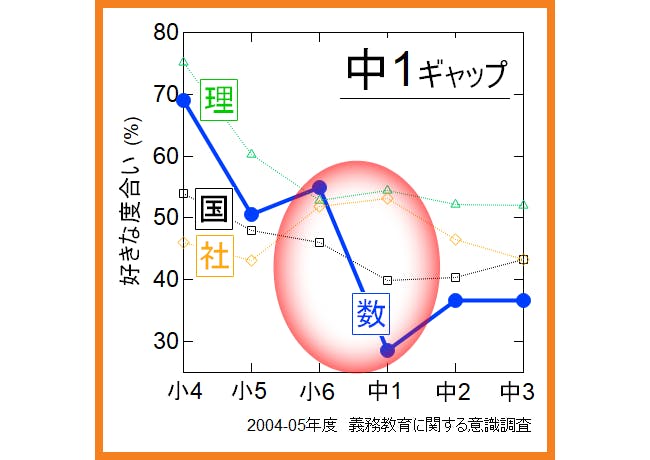
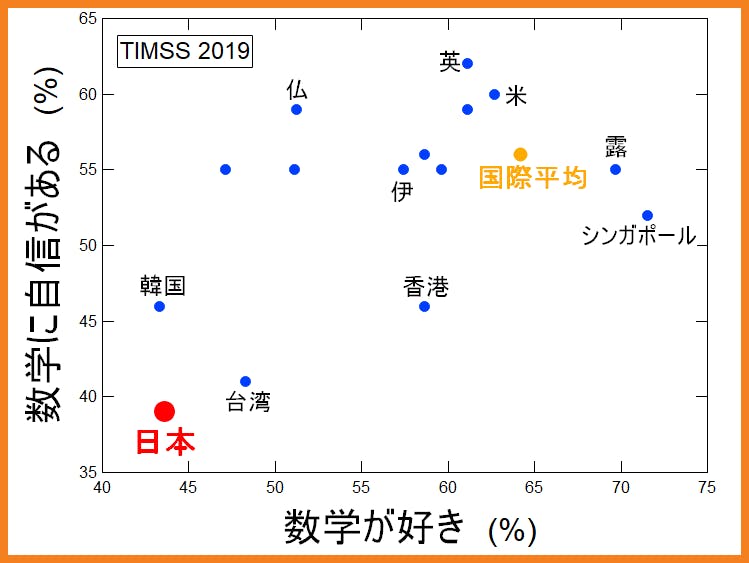
　脳科学者細田千尋氏が【経済力に1000万円の差｢数学コンプレックス｣が人生に及ぼす驚きの影響】という記事で数学に対する苦手意識についてのアメリカの研究成果を紹介しています。国際数学・理科教育動向調査(TIMSS)の2019調査結果によると日本は参加国中一番数学に自信がなく、数学が嫌いな子たちを輩出しています。その数学コンプレックスが収入に大きく関係しているという研究です。あなたが中学生の子を持つ方なら、自信を持った子に育ってほしいに違いありません。こどもの将来に大きくかかわっていく問題です。こどもに自信を持たせてあげたければ、数学応用問題を諦めさせるのではなく、「100人に1人しか解けなかった問題を解けた」という成功体験を持たせてあげることが大事だと思います。それにより、自信がつき、数学が好きになり、成績が向上し、より難問に挑戦し、さらに自信がつくという好循環が生まれます。基礎問題だけでなく応用問題をできるようになってもらいたい一番の理由は数学を通しての自己肯定です。今までの受験生ができていなかったといっても、考え方さえ理解すればそれほど難しくはありません。

　中1ギャップが生まれるのは、(マイナス)×(マイナス)を後ろ向きに進むとか、損の損は儲けになるとかの現実離れした例で教えるからで、わからなくなるのは当然です。小学校のかけ算から理解できていない。算数と中学数学の範囲内、少なくとも今問題にしている都立高校入試問題の応用問題では、１袋５個のみかんを４袋の場合は、5個/袋 ✕ 4袋 = 20個、長方形の面積の場合は、縦5cm ✕ 横4cm = 面積20㎠、など、計算結果の単位を変える異なる意味を持った数のかけ算、または、倍数、比率などの元の数の単位を変えない割合を変えるかけ算のみ扱い、同じ意味を持った数同士を掛けることはしません。a ✕ a の前と後ろの a は、量が同じなだけで違う意味を持つ a です。損の損という同じ質のかけ算をすること自体がおかしなことなので、それを例に出すことで、こどもたちは数学が理解できなくなってしまうのです。
　幼稚園児が遊びながら一次方程式を解けるようになる海外の iphone アプリがあります。そのアプリでのマイナスのかけ算の基本はオセロの駒です。マイナスのかけ算(わり算)１回ごとにオセロの駒を裏返しにするイメージをゲームで頭に刻み込ませています。このように扱いやすいイメージを持たせてやることが抽象的な数学の理解へとつながっていくんだと思います。運動会の紅白玉入れの結果発表なども紅と白(プラスとマイナス)１組ずつを相殺させて計算する例です。

　数学の応用問題ができないという統計結果は、難関校の難問の結果ではなくて一般の公立高校入試問題での結果なんです。しかも、学習塾で高校受験数学を習っているのにも関わらず「公立高校入試数学応用問題を誰もできない」というのはおかしいと思いませんか？「類題が繰り返し繰り返し出題」されているのにできていないんです。なぜ、学習塾は数学を国、英、社、理のように教えられないのでしょうか？その原因を解明し改革することがこどもたちを育てる社会の責務だと思います。こどもたち一人ひとりの人生は一度きりです。今すぐやらなければ、来年卒業する子たちは学ぶ機会を失われてしまいます。「どうせ誰もできないんなら応用問題なんてはじめから教えなければいい、日本に理工系なんてそんなに多く必要ない」という人もいるかもしれません。ひょっとすると、こどもの将来を考えることなく目先の試験合格に焦点を当て、時間がかかる応用問題は手を付けなくてもいいと教えている結果が基礎学習だけに集中して応用問題ができない理由なのかもしれません。しかし、教育委員会が解き方の違う問題ではなく、毎年毎年同じように解ける問題を出題しているわけは、教える側に対しては「応用問題も解答できるように教えられるはず」、そして受験生には「数学をちゃんと理解してほしい」というメッセージなのだと思います。

　この教育目標と入試結果のギャップを埋め、数学難民を救済するため、応用問題を解ける数学脳に作り変える講座を作成します。その結果、少しでも多くの子たちが数学を好きになってもらえることができればと期待しています。私は中学生を教えて名門高校に合格させた実績はありません。正直言って難関高校合格の確証はできません。しかし、物理学研究者としてこれまで大学生や大学院生を、記録写真家として社会人を教えて来た経験があります。500人規模の講演をしたことも、中国文化大学オープンカレッジで授業内容の優秀賞を頂いたこともあります。しかも、ここが大事なのですが、応用問題ができないこどもたちを今現在量産し続けている教える側の問題点を知っています。というより、理工系大学院卒にとってはあたりまえである考え方を生徒たちは学んでいません。それは市販の過去問集の解答を見れば明らかです。その考え方とはポリア教授の数学教育の歴史的名著「いかにして問題をとくか」をはじめとした国内外の数学教育書に書いてあることです。今回提示した応用問題が出来ていないという統計結果と学習参考書や高校過去問解説の解法内容、そしてyoutubeでの入試問題解説から推測されることは、これら数学教育者たちの言葉を教育現場では取り入れられていないんではということです。ポリア教授「いかにして問題をとくか」 の言葉を取り入れた中学数学の授業を行っている又は受けたことがあるという方はご連絡いただければ幸いです。

　クラウドファンディングを手段の第一歩とし「ずるい中学数学」オンライン講座を開発します。中３の平均教育費が37万円だそうです。教育格差が所得格差からという報告もあります。教育格差是正のため、難関校〇〇人合格をうたい文句とした高額講座ではなく、義務教育すべての生徒にこの講座が行き渡ることを目標とし、月額1000円(来年度より)という価格に設定しました。この教授内容が成功するかどうかはやってみなければわかりません。しかし、このままでは中学の段階で数学で挫折するこどもばかり送り出しているという「事実」は続いていきます。とはいうものの、一度に全員に行き渡らせることができない以上、初めのうちはこの講座を履修した受験生が数学応用問題に対して有利な立場に立ち、新たに情報格差による教育格差を生むこととなってしまいます。この「ずるい中学数学」を学びたい子たちに知ってもらうためには、中学校でチラシを配ることが一番効果的なのですが、教育委員会の許可をえるためには法人格である必要がありそうです。そのため、このプロジェクトの一番大きな出費は会社設立費とその維持費となります。このプロジェクトで示した数学教育の問題点に関心をもたれた教育委員の方々、または教育委員会または学校長にこの講座を推薦していただける方、こどもたちのため一緒に数学教育改革を行ってください。ご連絡お待ちしております。普及のための出張講演を行います。リターンに項目がありますので、応用問題を生徒に習得させたいと願う先生方、保護者の皆様、学習塾経営者、他、学校教育に関心のある方々のお申込みお待ちしております。また、講座内容を一緒に作ってみたいとお考えの若い教育者の方も歓迎します。いま、テレビドラマでも話題のEdTech(EducationとTechnologyをかけた造語)として、学習アプリが学校での補助教材として注目を集めるようになったように、補助教材として使ってみたいという方がいらっしゃれば、学校、学習塾、家庭教師、問わず歓迎いたします。多くのこどもが中学数学を楽しいと思える「ずるい中学数学」教育の普及にご賛同いただければ幸いです。

info@ezmath.jp

　算数と数学の違いは「ずるさ」にあります。中学数学の持つ「ずるさ」 とは、「問題文から数式への翻訳(立式)」と「その数式を解く計算」を明確に「分離」させることによって、数式への翻訳さえできれば「一気に解ける」状態にすることです。これを「代数は逆の方向に進む」 とニュートンは言い、アインシュタイン少年は「代数はずるい算数」と教えられました。湯川秀樹博士も「(算数では)まるで手品のような巧妙な工夫をしないと、答えが出ない問題(を、代数では)苦もなく解ける」 と書かれています。算数と数学の考え方の明確な区別を教える側ができないかぎり、こどもたちが応用問題を解けるようになるのは難しいといえます。

　応用問題は複数の条件が課せられた問題です。教える側の問題点は、応用問題をまるでゲームのように、一つずつ「場面をクリアし、その結果を使い、次の扉を選択し開ける」というプロセスをいくつか経て初めて答えが求まるという算数的立場に立って数学を教えていることです。湯川秀樹博士のいう「手品のような巧妙な工夫」です。途中どこかで場面クリアできない又は扉を選択できない、つまり、行き詰まった段階でゲームオーバーです。まるで、算数の特殊算のように、「思い付きの連続」に結果が左右されるから数学に自信が持てないという生徒が量産されてしまうんです。講座では実例を挙げ「ずるい数学」と「特殊算的数学」の違いを説明します。

　与えられた条件から直接答えが求まる基礎問題に対して、応用問題は複数の条件を満たすような答えを問う問題です。

なぜ基礎問題しかできないかを推測すると、ラスボスが代数だと二次方程式の解の公式、図形だと三平方の定理のように、中学数学を学ぶ目的を公式を導き出すことに置いているからだと思っています。その公式を定着させるために練習問題を行っています。しかし、公式は問題を解くための武器にしかすぎず、それを目的としたのでは、何のために数学を習っているのかわからず、やる気が出なくなるのは当たり前です。武器を手に入れてからが中学数学の始まりで、その面白さを伝えられるかどうかが数学教育者の務めだと信じています。先生たちがよりわかりやすい教授法をお互いもっと議論しあえる環境を作っていくことが、こどもたちの数学コンプレックス解消につながるんではないでしょうか。

　次に応用問題の簡単な例を示します。都立入試問題の一部を抜き出し改題したものです。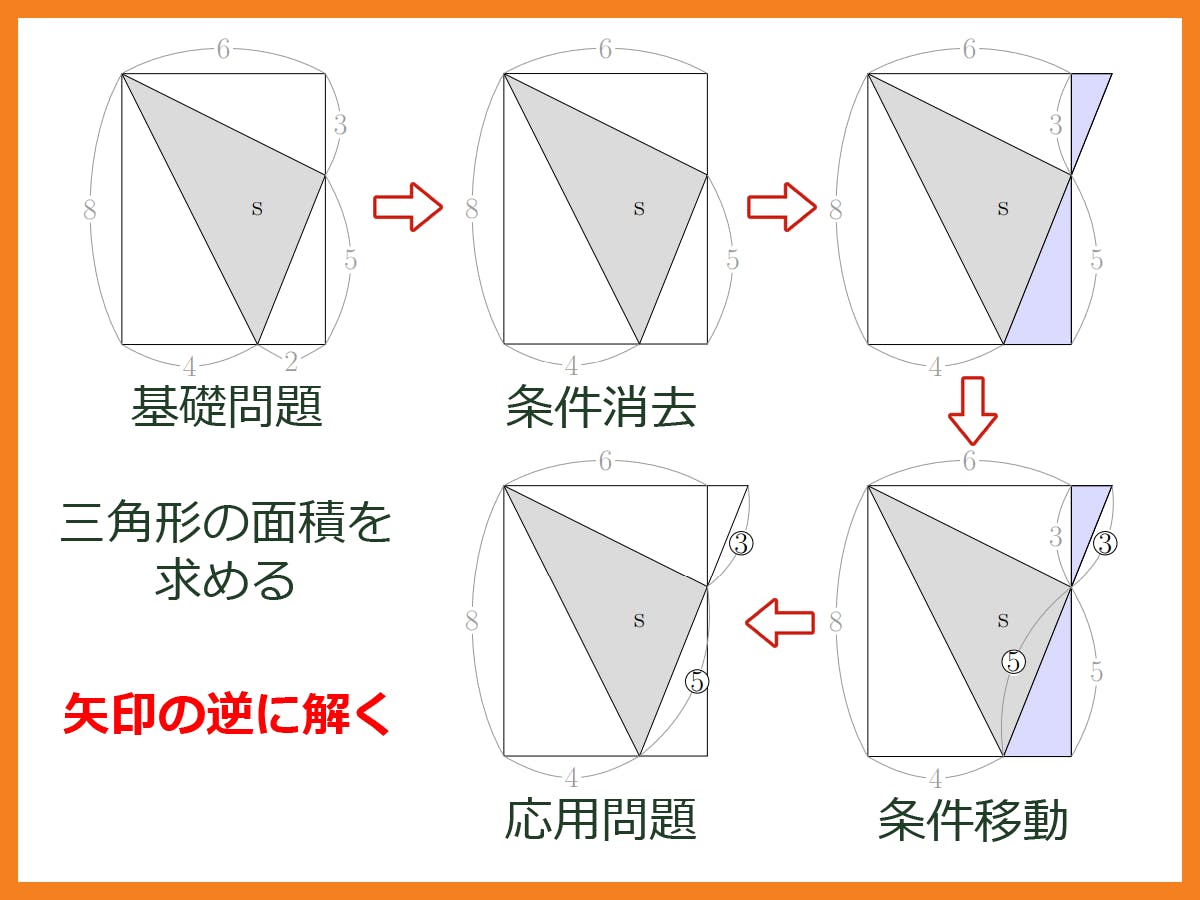

「直方体に内接する三角形の面積を求める基礎問題」

長方形の面積から３つの直角三角形の面積を引いて求めます。

この問題を難しくしていきましょう。

まず、図中の値 3と2 の条件はすぐに求められるので消去します

残った8, 6, 4, 5 の内１つを他の条件から求めるように書き換え、消去します。例として5を消去。

三角形と長方形の辺を伸ばし直角三角形を作ってやり、相似三角形の条件から、3と5を別の場所に移すことにより、簡単な応用問題が出来上がります。

問題を作った順の逆をたどれば解くことが出来ます。

応用問題を見ての着眼点は基礎問題の3または5、そのどちらかの位置にある値です。これが無いと三角形の面積が求まらないので、この数字をどこかから引っ張ってくる。

与えられている条件は３：５なので、これを使って基礎問題の３または５の位置に入る値を求める。

応用問題は問題を解くのに必要だけど与えられてはいない値を、別の条件を使って求める問題です。

この考え方を教えてさえいれば、応用問題を解ける生徒がこんなに少なくはないはずです。これを繰り返せば応用問題も十分得点できるでしょう。

ここまでは、「ずるい数学」を使っていません。「ずるい数学」を使うと、図中の矢印(道筋)とは関係なく 考え始めることが出来ます。

「ずるい数学」は、問題を出題条件ごとに分割し、各条件を方程式に「翻訳」し、連立方程式を「計算」することです。

各条件の「翻訳」さえできれば、あとは機械的に解けてしまいます。

　計算力を鍛える必要がある代わりに、大きな問題全体の道筋を考える必要がなくなります。

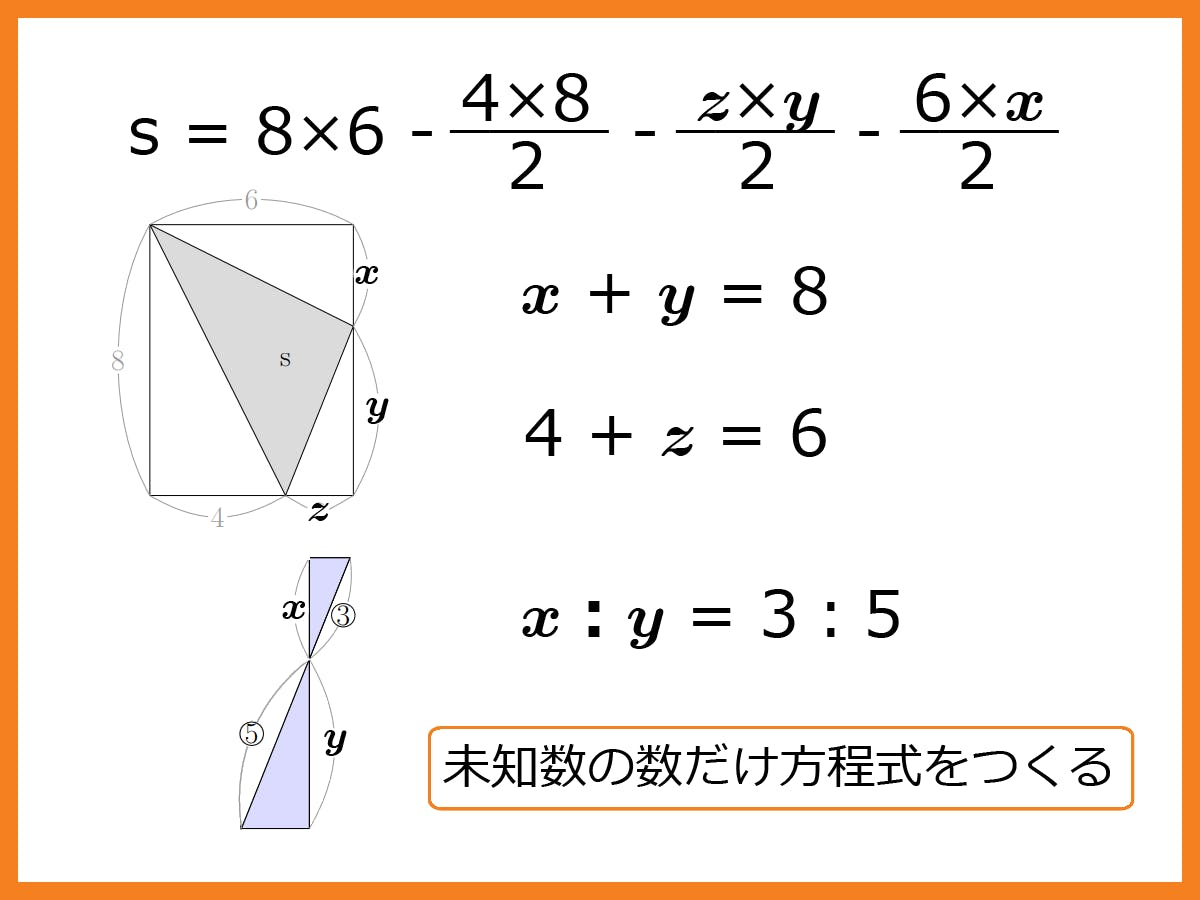
どうですか？難しいですか？一つ一つの翻訳は難しくはないはずです。応用問題で難しいのは道筋を立てることです。その難しいところを、やめてしまえというのが「ずるい数学」です。「ずるさ」をこの講座で学んでください。

　どの様な問題例がいいのか迷った結果、ポリア教授の「問題を変形させること、問題をいいかえること」を学べる良問で、しかも予備知識なしで小学生でも解き方がわかってしまう問題を選びました。正解が100人に2.4人と極めて低いのにもかかわらず、誰でも考え方を理解できる立体の問題(大問５)です。

市販の過去問集の解答で学んだ受験生がなぜ受験当日にこの問題ができなかったのか？その理由は計算量です。どの解説も試験時間内に終わらすことが難しい計算をさせています。たとえ解き方を理解していたとしても、その計算量のため正答できないでしょう。その対策を短時間で学べます。

「直方体に内接する四角すいの体積を求める問題」

この例題から学べること

(1) 考えやすい問題に書き換える。

(2) 計算しやすい基準との割合を求める。よく使われる面積の基準は東京ドーム(東京ドーム10個分とか)

(3) 仲介を通して与えられた値と解答をつなげる

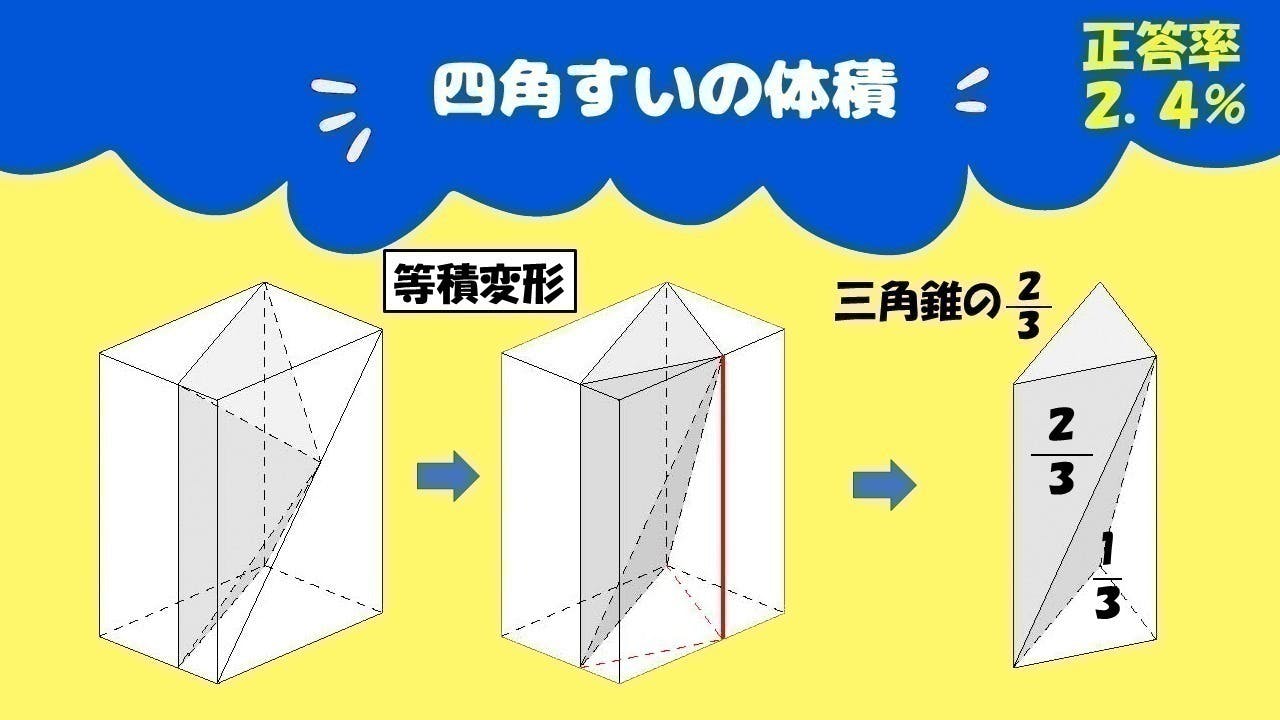
100人に2.4人しか答えられなかった四角すいの体積を求める問題

(1) 底面積と高さが同じ、つまり同じ体積の四角すいへ変形(等積変形)する。
(2) 三角柱との体積比から四角すいの体積を求める。
(3) 四角すいは三角柱から三角すい(仲介)を引いたもので、三角すいは三角柱の体積Vの1/3なので、残りの2/3が四角すいの体積

ここまで書き換えられれば、四角すいの体積vは、

v=(2/3)三角柱V=(2/3)底面積s×高さ12

s を計算すれば求まる。

　「問題を変形させること、問題をいいかえること」は中学数学に限ったことではありません。こどもたちが社会に出ていろいろな分野で問題に遭遇します。その問題は全く新しい問題ではなく、どこかで誰かが解決したことがある問題です。それに気づきさえすれば先人の成果が利用できるようになります。しかし、全く同じ形ということはなく、先人の成果を使うためには、同じ解き方ができると気がつかなければならず、かつ、その形へと書き換えてやる必要があります。その書き換えの訓練を受けていなければ自力で解こうと立ち止まってしまいます。中学数学を学ぶ理由の一つとして、この「問題を変形させること、問題をいいかえること」の訓練がほかの科目よりはるかに効率的に行えるということが挙げられるでしょう。ちょうどスポーツ選手の筋トレやランニングと同じで、効率がいいから行っているんです。応用問題の書き換えを教えないということは、こどもたちが中学数学を学ぶことで得られる大きな利益の一つを、教える側は与える必要はないと判断してしまっているということになります。
　「社会に出ても数学は使われないんだ」という考えをこどもたちが持ちながら数学を学んでいる限り、学習意欲がなくなっていき、数学に自信が持てなくなるという悪循環が生まれます。数学を学ぶ意義を伝えない「教える側の態度」が国英社理の入試結果のように正常な正規分布にならない数学だけの異常な統計結果に反映されているのでしょう。この現状を知ったことがこのプロジェクトを思い立ち成功させたい理由です。このままではいけないと思われた先生方、塾の講師陣、こどもたちのために一緒にこの状況を変えていきましょう。ご連絡お待ちしております。中学生のお子さんを持つ方、応用問題を難なくこなせるように育て、こどもに理系に進むというもう一つの選択肢も与えてやってください。中学の段階で応用問題ができないという現状から判断して、このまま大学まで進んでもほとんどの子は理系の講義を消化できないことでしょう。

　ポリア教授の言葉は、「問題をいいかえること」だけではありません。例えば都立高校入試の平面図形(大問4)の問題は辺の長さが既知の三角形と求めたい辺の長さを１辺に持つ三角形が直接結びつかず、難問といえます。ここでは「補助要素の導入」の考え方が使えます。仲介役の三角形を通して答えを導き出します。ちょうど、目的地に行くのに、地図を仲介として計画をたて、現実に戻って計画を実行することに似ています。ちなみに、地図を使うのは「問題をいいかえること」でもあります。

　一つ一つ全く違った問題ではなく同じ解き方の問題が毎年出題されているのは、数学を学ぶ上でのいくつかの重要な考え方を学ばせたいという出題者の思いが詰まっているのだと思います。都立(公立)高校入試の応用問題は学ぶに値する問題です。それを今までずっと対策を講じず捨ててきたのはもったいないと思いませんか？このプロジェクトを通して、こどもたちだけではなく、教える側の意識改革もできたらと願っています。
　ポリア教授の言葉、その一言一言が数学を学ぶ意義を指し示しています。ポリア教授の言葉を頭に刻み、言葉通りに問題と向き合うことで応用問題も解けるようになります。そのために、良問だらけの公立高校入試問題を例題にして、一つ一つ解説をしていく講座にしていきます。

① 都立高校入試過去問解説書

自費出版書１冊 2,000円(送料込)
内容はほぼ書き上がっています。解説160ページ程度のカラー刷り、別冊問題白黒40ページで、お申し込み人数を見て印刷発注致します。
10月上旬発送

② オンライン講座

１講座あたり 2,000円、全５講座
　中学数学３年分を都立高校入試問題に従い全５講座に分け、１講座は短い動画の合計を4時間から8時間程度を予定しています。よくある間違いを指摘し、その間違いを起こさないような考え方が身につくような講義にします。今回お申し込みの方は１講座あたり2000円で中学校卒業まで、または小中学生以外の方は一年間の使用とします。大手のオンライン学習サービスに倣い来年１月の新規登録者より月額課金制に移行します。月額1000円の予定です。
　第１講座は小学一年生の足算から考え方を教えていきます。特に約分や通分でよく計算ミスを起こす子は「かたまり」と「分割」のイメージが出来ていないことが原因と思われます。そのイメージづくりの教材から作っていきます。その他は都立高校入試過去問解説を使った内容で、基礎部分の解説をより詳しく付け加えるだけなので、構想はほぼできています。今回、苦手な分野だけのお申し込みも可能ですが、第１講座は学習することをオススメします。第１講座は２次方程式までの計算ですが、中１の生徒も無理なく学習できるような基礎講座で算数から始めます。来年２，３月の高校入試に間に合わせるため、できれば冬休み終わりまでに中学数学全範囲を一通り学んでほしいので、講義内容は学校の授業より早く進んでいます。「単位変換と比率」「変形」「中継」「検算」そして「翻訳と計算の分離」など将来にわたって使える「こんなやり方があったのか」と思える考え方を基礎から訓練することで、応用問題も実はそんなに難しくないと思える数学脳が身につくような講座にします。

副教材として使っていただける先生方は、500円ご支援又は500円講演依頼の備考欄にてお問い合わせください。教材用として別途配布いたします。

全講座まとめ買い 限定1名 2,000円

全講座まとめ買い 限定3名 3,000円

全講座まとめ買い 限定5名 4,000円

全講座まとめ買い 限定120名 5,000円

全講座まとめ買い 限定200名 7,000円

団体購入　人数無制限　300,000円

協力　全講座　10,000円
　参画、協力していただける方

③ 出張講演依頼 限定100名 500円
　１時間の出張講演をお受けします。
　参加人数：30名以上
　内容、日時はご相談に応じます。
　教育改革の草の根運動です。ご賛同いただければ幸いです。
　備考欄におおよその講演項目(例、二次関数)ご記入ください
　別途東京からの交通費・滞在費を実費で後日銀行振込でいただきます。

【応援型メニュー】 

ご協力

④ 御礼のメール   500円

⑤ 協賛　500,000万円
　 団体、企業、個人での協賛。
「ずるい数学」ウェブサイト(企画中)に協賛としてインタビューコーナーを設けさせていただきます。また、講演会などで協賛の提示をさせていただきます。その他、ご要望がありましたらお申し出ください。ご希望に沿うよう努力いたします。　　
賛金として集めた援助金は全額、広告、広報資金に使用させていただきます。逐次成果報告書を提出いたします。

  9月上旬 第一章 計算
10月上旬 第二章 文章題
11月上旬 第三章 関数
12月上旬 第四章 平面図形
12月下旬 第五章 立体図形

Kajabi という世界中で使われている信頼性の高いオンラインスクールプラットホームを利用して動画を配信します。メールにてIDを発行します。Kajabi の利点は iOS, Androidに対応したスマホアプリが用意されていることです。大手オンラインスクールのように ID, パスワードの入力で使用できます。自社製のアプリ開発によるバグの心配がありません。また、Kajabi にはコーチング機能やコミュニティ機能が備わっていて、個別質問に答えられる機能や生徒同士の交流など利用者のニーズに合った機能を追加することができます。
目標額に達しなかった場合でも計画は実行いたします。

<リターン履行に遅延が生じた場合>

入試という期限付きの案件である以上、配信の遅延は許されることではありません。しかし、不慮の事故のため万一遅延が生じた場合、オンライン講座お申し込みの方に全額返金の保証を致します。

<リターン履行に必要な法に基づく業務資格>

このプロジェクトには法的規制はありません。
また、中学校教員免許は取得しておりませんが、大学生、大学院生、社会人を指導た経験があります。

法人格以外は教育委員会など公共機関との交渉は難しく、アマゾンpayや広告PRなど運営面でも支障をきたすため、会社設立をすることにしました。その資金の一部として使わせていただきます。

過去問解説書500冊の印刷費及び送料：約70万円
会社設立費：約30万円
事務所兼教室賃料及び設備費：約100万円
運営維持費、製作費、人件費、その他：600万円以上
広報宣伝費：約200万円
Campfire手数料：約100万円

＜募集方式について＞
本プロジェクトはAll-in方式で実施します。目標金額に満たない場合も、計画を実行し、リターンをお届けします。