
昨日は公開研究会があり、参会させていただきました!
またまた非常に勉強になりました!
私は中学校2年生の数学(図形)の授業と、高校2年生の数学(指数関数)の授業を見学しました。
それぞれに大きな学びがありましたので、今日は中学2年生の図形の授業での学びを書きます。
筆者が今回学んだのは、
1.(良い意味での)「緩い共有」
2.自ら答えを出すために探究する文化
の学びへの寄与の在り方でした。
上の学びを説明するには、授業の特徴を把握している必要がありますので、まずは見学した授業の特徴を記載します。
今回見学した授業の特徴は、グループ・個人の混同した学びを軸としつつ、適宜その学びを支援する形で全体での学びが入っている点が挙げられます。
まず今回、見学した東大附属の教室の特徴として、中央の空かないコの字型で終始授業が行われていました。【図1】
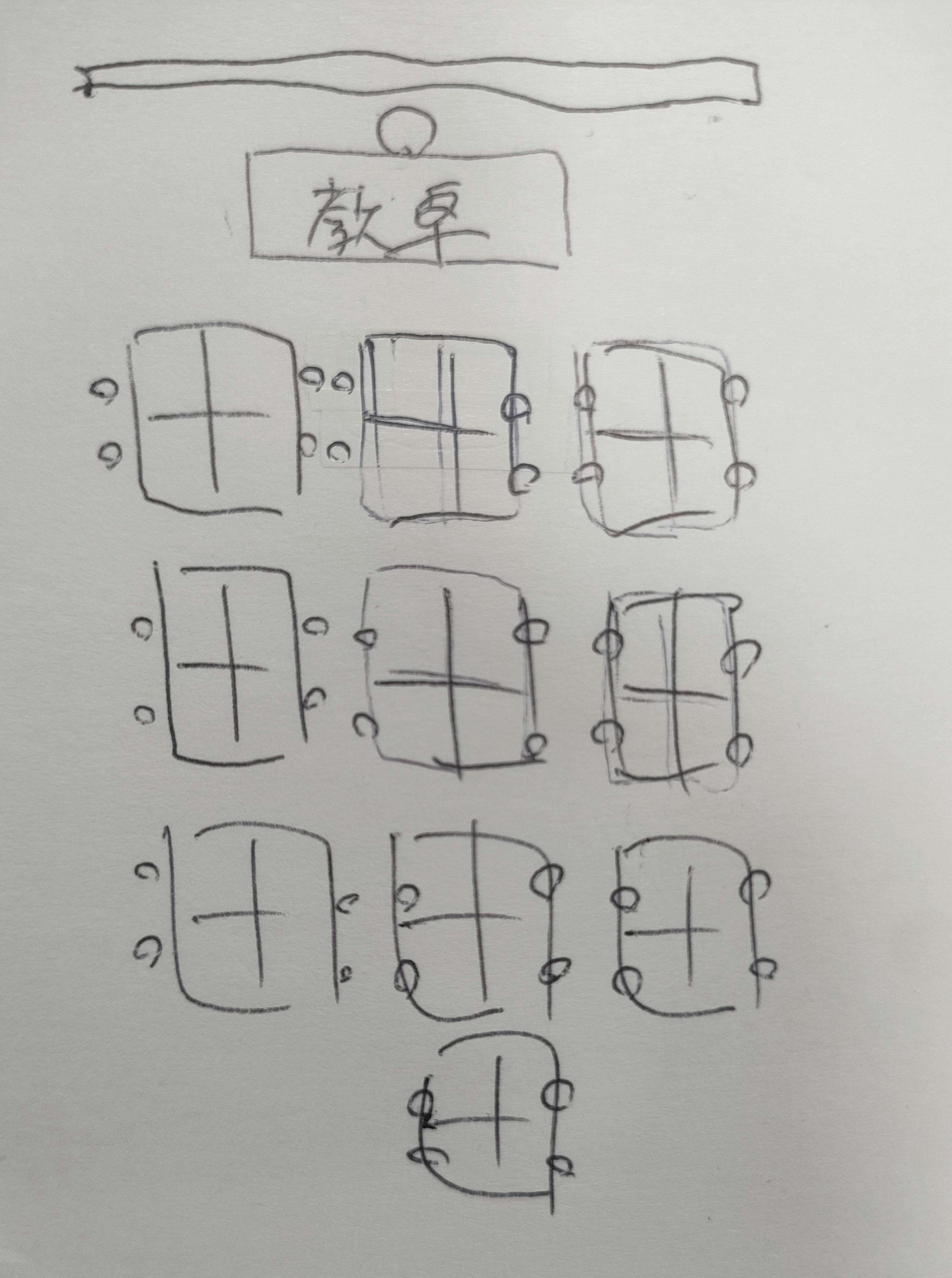
【図1】
また授業は、メインの問いが最初に投げかけられ、50分間の探究で様々な性質を見出しつつ、その問いの解決が進んでいきました。具体的には、教師が黒板に大きな三角形ABCを書き、各頂点から垂線を下ろし、それらの垂線の足(垂線と三角形の各辺の交点)をそれぞれ点D, E, Fとし、D,E,Fをすべて結び垂足三角形を作図し、「△ABCの垂心は△DEFにとっては何心?」という発問により個人とグループの混ざった検討が始まる授業でした。【図2】
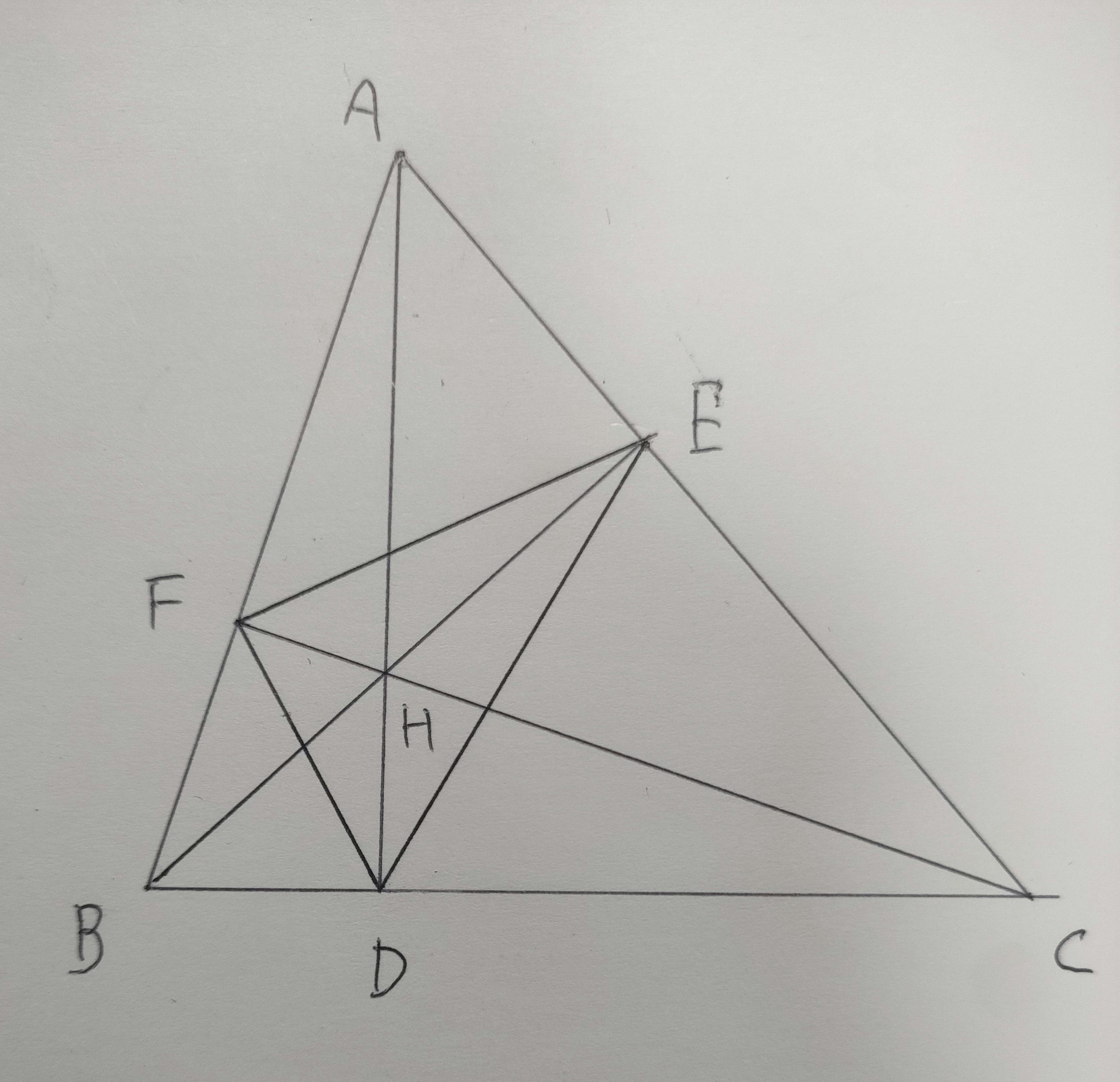
【図2】
ここでの学びで、生徒は自分の考えを軸としつつ、グループにて友人の考えを聞いたり、自分の考えを話しつつ整理したりし、探究を進めていました。また、度々探究が停滞するも、その都度教室全体での考えの共有がタイミングよく入り、探究を進める参考知見を得て、また自分の考えをグループでの検討と適宜混ぜつつ進めていました。
その結果、自分の考えを軸としつつ、適度に探究を進めること、全体での解決を聞き、驚くことにつながっていました(自身の力で解決できた生徒は、感動していました)。
今回の課題はなかなかに難しく、与えられた条件から証明したい性質までに距離があり、腰のすえた探究が求められます。具体的には、「△ABCの垂心が△DEFの内心であることを示す」→「∠EFH=∠DFHを示せばよい(他の頂角についても同様より)」→「(垂心の定義より)∠AEH=∠AFHなので)4点A, E, H, Fを通る円が書ける」→「(円周角の定理より)∠HAE=∠HFE」→「(同様にして)∠HFD=∠HBD」→「(垂心の定義より)4点A,E,D,Bを通る円が書ける」→「(円周角の定理より)∠DAE=∠DBE」→「よって、∠EFH=∠DFH」という流れで証明がなされました。【図3】
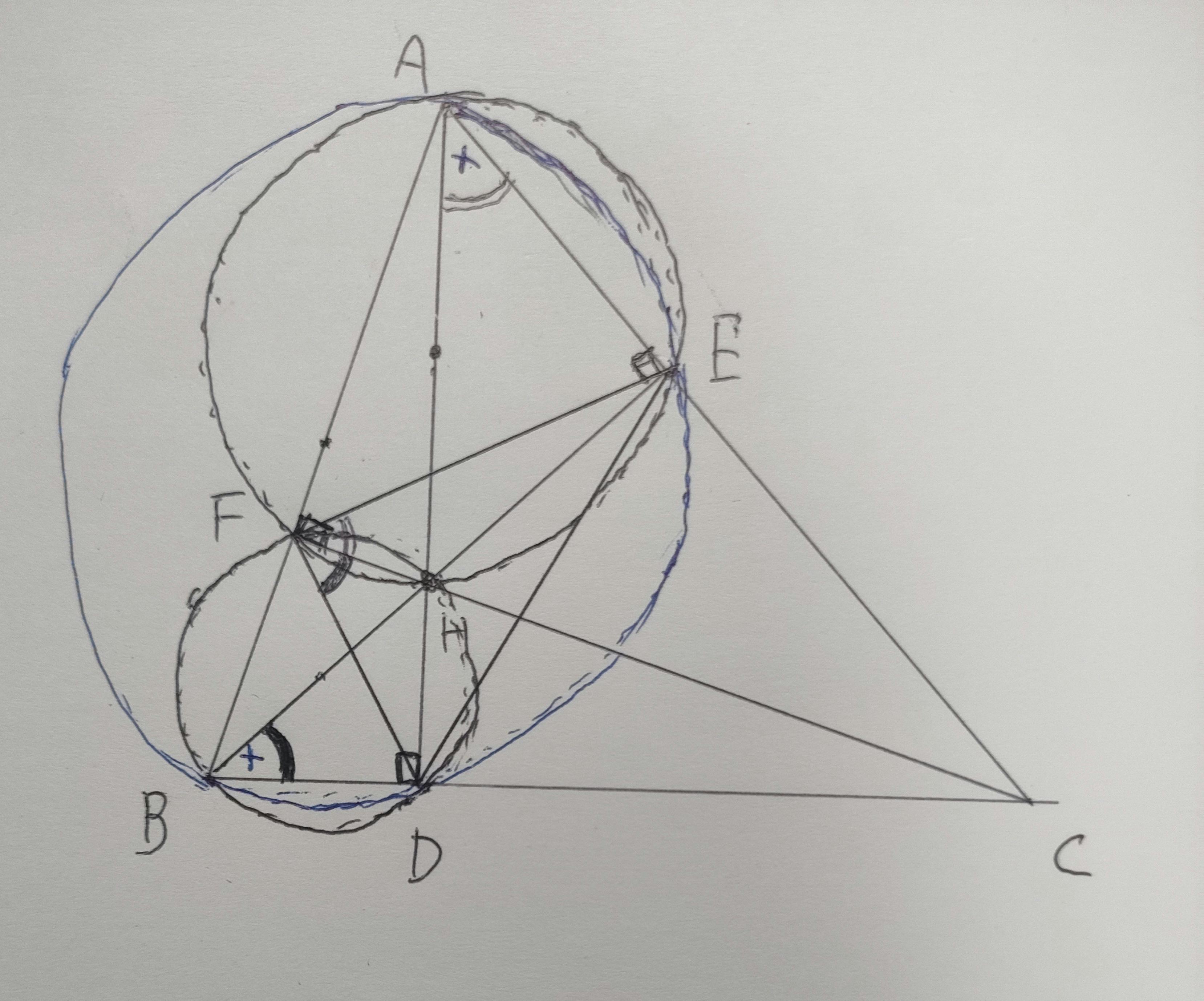
【図3】
「1.(良い意味での)『緩い共有』の学びへの寄与」を感じたのは、グループと個人の混同した学びを軸としつつ、全体場面での「緩い共有」の場面でした。
私が教員のころは全体での話をしっかりと聞かせるべく、生徒全員の作業を止めさせ、目線を黒板に集めさせたうえで、生徒を指名し、意見を聞き、張った声でその意見を復唱していました。しかし、東大附属のその先生は、強い方向付けはせず、落ち着いた声で「この点は三角形DEFの何心なの?」「(内心ではないかという生徒の意見に対して)内心だと何を示せればよいの?」と尋ね、「じゃあ、もうちょっと頑張ってみようか」と生徒の探究に戻します。そして、授業は終始ゆったりと落ち着いた雰囲気で進んでいました。
ここでは生徒は自分の考えを軸としつつ、グループからの支援、グループでの考えの共有を行いつつ、全体の意見を必要に応じて取り入れていました。そのため、全体の指示での方向づけの力は弱く、あくまでも自分の探究が軸であり続けました。これが自分を軸とした対象の図形の性質の発見やつながりを生んでいました。
確かに教師による「正答」の方向付けが弱いため、正しい解答に「効率的な」手順では進まない場面も多いでしょう。今回、私が見ていたグループも自力では「正解」にはたどり着いていませんでした。
しかし、自力で解けなかった生徒も、正しい解答の後追いではなく、自分なりの探究が土台にあり、その上でできた生徒の考えを聞いており、それがその性質の証明への感動を生んでいました。
教師による段階的なヒントによる方向付けは、確かに問題解決を効率的に進めるでしょう。一方で、その対象(今回であれば対象の図形)そのものへの検討が不十分にさせる危険性もはらんでいると感じました。道を歩くときに足裏部分の地面だけでは不安であり、やはり道全体の地面がある方が安心できるように、問題解決も解答部分だけの知識だけではなく、その探究過程で見出した試行錯誤や性質が必要だと思わされました。(この点は指摘されると同意するのですが、実践ではついつい正しい解答を最短で理解させる方向にすすんでしまうんですよね。でも、それでは数学を味わっていないので、あんまりおもしろくない(効率的に解けるようになったという水準で終わってしまう)と)
確かに時間を言い訳にして、ついつい教え込みをしたくなりますが、今回のようなその図形の性質を味わうための授業では、意味のある探究の時間が必要不可欠なのでしょう。やはり砂糖水を飲むための砂糖が水に溶けるのを待つ時間が必要ということなのでしょう。
そして、上の学びを支えているのは、「2.自ら答えを出すために探究する文化」でした。
今回見学した授業でも、その次の授業でも、生徒は自ら答えを出すことを目指しておりました。授業でよくみられる風景である、授業の半ばまではぼうっと過ごし、授業のまとめの際に効率よく授業内容を習得しようという生徒や、問題探究を放棄し、最終的には教師から提示されるであろう模範解答を待つ生徒は見られませんでした。
これは学校全体で答えを待たせる授業ではなく、自ら検討しなければ得られないような授業を目指して実践を行っており、自分なりの探究で自分なりの発見に到達することを目指す文化の影響もあるでしょう。
またその文化の上で、教科単位にて、探究に値する問いを提案し、その探究を各々が取り組めるように個人とグループの混同した探究形態をとること、個人の探究を断絶しない「緩い」全体共有などが行われ続けていること、5分、10分での短い問題解決ではなく、大きな考える価値ある問いを、じっくりと問題場面を探究する形で検討する投げかけの影響も大きいのだろうと感じました。
答えは教師が出すのではなく、「自分で出す」という授業の継続が、今回の授業で見られた生徒が自らの探究する力を養っていると感じました。
この授業では、生徒が自ら問題を探究し、周辺情報も含めた探究を行うことで、その問題の情景を捉え、その性質を知ったときの感動を生じさせ、数学を味わうような探究が見られました。もちろん探究の力がまだこれからの生徒もおりましたが、東大附属のもつ自分とグループの混同した学びの中で、全体共緩やかにつながる空間は、そんな生徒の探究の力の素地を着実に作っていると感じさせるものでした。
なんとも良い時間を過ごさせていただきました。








